Unidad 5

Sistema tridimensional 

Un objeto es tridimensional si tiene tres dimensiones. Es decir cada uno de sus puntos puede ser localizado especificando tres números dentro de un cierto rango. El sistema tridimensional mas usado en física (clásica) es el espacio: una dimension para el ancho, otra para la altura y otro para la profundidad. Para representarlo basta con el grafico de ejes cartesianos X,Y,Z. En las imágenes se puede observar el grafico con el que se representan los sistemas tridimensionales.

Ejercicios 

• Un ejercicio práctico de sistema de coordenadas tridimensionales, se puede ver en el computador al diseñar un cubo en tres dimensiones y que este pueda moverse a través de un programa.

Lo primero que se debe hacer es ubicar las coordenadas de los puntos principales del cubo.

Observa que el centro del sistema en este caso está ubicado en el centro del cubo donde se trazaron los ejes X, Y y Z.

• Un cubo tiene una arista de 8 unidades y se ubica en el sistema cartesiano tal como se ilustra en la siguiente figura. ¿Cuáles son las coordenadas del punto P? 

En la figura, se cumple que x = 0; y = 8 y z = 8,

Por tanto, sus coordenadas son (0, 8, 8).

 - ¿Cuál será la medida del trazo OP? ¿Y el trazo OA?

Si observas la figura, identificarás que el trazo OP es la diagonal de una de sus caras. Como cada arista mide 8, entonces:

El trazo OA es la diagonal principal del cubo, y aplicando, a partir del cálculo anterior, el Teorema de Pitágoras en el triángulo que se forma en el espacio OAP, tenemos que:

En general, podemos determinar que la diagonal principal de un cubo de lado a es igual a:

Más generalizado, podemos determinar que la diagonal principal de un paralelogramo

de largo a, ancho b y  altura c tiene la forma .

Ejemplo

La diagonal principal de un paralelepípedo de lados  5, 10 y 12, tiene el valor de

Poliedros

Un políedro es la región del espacio delimitada por polígonos, o lo que es lo mismo, un cuerpo geométrico cuyas caras son planas que encierran un volumen finito.

• ·         Caras: Cada uno de los polígonos que limitan el poliedro

• ·         Aristas: Los lados de las caras del poliedro. Dos caras tienen una arista en común.

• ·         Vértices: Los vértices de cada una de las caras del poliedro. Tres caras coinciden en un mismo vértice.

• ·         Ángulos diedros: Ángulos formados por cada dos caras que tienen una arista en común.

• ·         Ángulos poliédricos: Los ángulos formados por tres o más caras del poliedro con un vértice común.

• ·         Diagonales: Segmentos que unen dos vértices no pertenecientes a la misma cara.

Clasificación y familias de poliedros

Los poliedros pueden ser clasificados en muchos grupos según la familia dónde provienen o de las características que los diferencian.

Según sus características, se distinguen:

• En un poliedro convexo una recta sólo pueda cortar a su superficie en dos puntos.
  
• En un poliedro cóncavo una recta puede cortar su superficie en más de dos puntos, por lo que posee algún ángulo diedro entrante.
  
• En un poliedro de caras uniformes todas las caras son iguales.
  
• Se dice poliedro de aristas uniformes cuando en todas sus aristas se reúnen el mismo par de caras.
  
• Se dice poliedro de vértices uniforme cuando en todos los vértices del poliedro convergen el mismo número de caras y en el mismo orden.
  

Estos grupos no son exclusivos, es decir, un poliedro puede estar incluido en más de uno de ellos.

Además de las clasificaciones anteriores, también podemos clasificar los poliedros mediante sus familias:

• Poliedros regulares: Son los llamados sólidos platónicos.
  
• Poliedros irregulares
  • Los sólidos arquimedianos son poliedros convexos de caras regulares y vértices uniformes pero de caras no uniformes.
  
  • Los prismas y los antiprismas son los únicos poliedros convexos y uniformes restantes. Todos los prismas se construyen con dos caras paralelas llamadas directrices que le dan el nombre al prisma y una serie de paralelogramos, tantos como lados tenga la cara directriz.
  
  • Los sólidos de Johnson son los poliedros convexos, de caras regulares restantes, sólo uno de ellos es uniforme.
  
  • Las bipirámides y trapezoedros son poliedros de caras uniformes pero no son de caras regulares, ni de vértices o aristas uniformes.
  
  • Los sólidos de Catalan son poliedros de caras no regulares y no todas sus caras son uniformes.
  
  •  Deltaedros  cuerpo que sólo están formado por triángulos equiláteros, no constituyen un grupo excluyente de sólidos.
  

Ejercicios

Sólidos de revolución

Un sólido de revolución es un cuerpo que puede obtenerse mediante una operación geométrica de rotación de una superficie plana alrededor de una recta que se contenida en su mismo plano. En principio, cualquier cuerpo con simetría axial o cilíndrica es un sólido de revolución.

Se denomina sólido de revolución o volumen de revolución, al sólido obtenido al rotar una región del plano alrededor de una recta ubicada en el mismo, las cuales pueden o no cruzarse. Dicha recta se denomina eje de revolución.

Sea f una función continua y positiva en el intervalo [a,b]. Si la región R indicada en la figura rota alrededor del eje X, ésta genera un sólido de revolución cuyo volumen tratamos de determinar.

Rotaciones alrededor de los ejes cartesianos

El volumen de los sólidos generados por revolución alrededor de los ejes cartesianos se pueden obtener mediante las siguientes ecuaciones cuadráticas.

Rotación paralela al eje (x)

El volumen de un sólido generado por el giro de un área comprendida entre dos gráficas, f(x) y g(x) definidas en un intervalo [a,b] alrededor de un eje horizontal, es decir, una recta paralela al eje OX de expresión y=K siendo K constante, viene dado por la siguiente fórmula genérica

${\displaystyle V=\pi \int _{a}^{b}([f(x)-K]^{2}-[g(x)-K]^{2})\,dx}$

En particular, si se gira una figura plana comprendida entre y = f(x), y = 0, x = a y x = b alrededor del eje OX, el volumen del sólido de revolución viene generado por la fórmula:

${\displaystyle V=\pi \int _{a}^{b}f^{2}(x)\,dx}$ método de discos.

Ambas expresiones se deducen de que al hacer girar un área formada por innumerables rectángulos de base dxy altura f(x), alrededor del eje X, se forman discos colocados verticalmente cuyos volúmenes sumados resultan en el volumen de todo el sólido. Cada disco tiene por volumen el de un cilindro como si fuera una moneda acomodada verticalmente, es decir, V=Πr²h donde el radio de la base del cilindro es f(x), y la altura del cilindro es dx, por lo que el volumen del cilindro resulta ser V = πf²(x)dx y la suma de todos estos volúmenes parciales, es el volumen total que resulta en la expresión:

${\displaystyle V=\pi \int _{a}^{b}f^{2}(x)\,{\text{d}}x}$

Si son dos funciones f(x) y g(x), el volumen total será la resta del volumen mayor menos el volumen menor

${\displaystyle V=\pi \int _{a}^{b}([f(x)]^{2}-[g(x)]^{2})\,dx}$

Pero si el giro es alrededor de una recta paralela al eje X: y=K, entonces la expresión resultante es (siempre que K<X en para todo X):

${\displaystyle V=\pi \int _{a}^{b}([f(x)-K]^{2}-[g(x)-K]^{2})\,dx}$

en el caso en el que K>X, es decir la recta y=K que se encuentre debajo de las funciones, se debe aplicar:

${\displaystyle V=\pi \int _{a}^{b}([K-f(x)]^{2}-[K-g(x)]^{2})\,dx}$

Rotación paralela al eje de ordenadas (Eje y)

Éste es otro método permite la obtención de volúmenes generados por el giro de un área comprendida entre dos funciones cualesquiera, f(x) y g(x), en un intervalo [a,b], con f(x) > g(x) en el intervalo [a,b].Alrededor de un eje de revolución paralelo al eje de ordenadas cuya expresión es x=K siendo K constante positiva. La fórmula general del volumen de estos sólidos es:

${\displaystyle V=2\pi \int _{a}^{b}(x-k)[f(x)-g(x)]\,dx}$

Nótese que ${\displaystyle x-k>0}$, por ende, esta fórmula funciona si la recta se encuentra a la izquierda de la región R comprendida entre las curvas f(x) y g(x), para que nuestra integral sea positiva.

Esta fórmula se simplifica si giramos la figura plana comprendida entre y=f(x), y=0, x=a y x=b alrededor del eje OY, ya que el volumen del sólido de revolución viene generado por:

${\displaystyle V=2\pi \int _{a}^{b}xf(x)\,dx}$ (método de cilindros o capas)

EJERCICIOS

Poliedros y cuerpos redondos 

Los cuerpos geométricos, y demás figuras geométricas en general, se estudian con profundidad en matemáticas. Pero también en el arte hace falta tener unos conocimientos básicos de geometría para describir una obra de arte, planificar su construcción o realizar dibujos técnicos.

Cuerpos geométricos: Definición y clasificación

Un cuerpo geométrico es una figura geométrica con tres dimensiones: altura, longitud y ancho (o profundidad).

Entendido como lugar geométrico un cuerpo sólido es un área con volumen cerrada por superficies en un espacio tridimensional.

Los cuerpos geométricos se dividen principalmente en dos tipos dependiendo de si sus superficies son planas o curvas: Poliedros y cuerpos redondos.

Poliedros: Definición, tipos y nombres

Poliedro es el cuerpo geométrico delimitado tan solo por polígonos siendo por lo tanto planas todas sus caras. Los poliedros -o cuerpos planos- se clasifican a su vez en dos tipos:

1. Poliedros regulares, también llamados sólidos platónicos, son aquellos cuyas caras son polígonos regulares iguales, del mismo tamaño, con vértices en los que concurren el mismo número de caras y con ángulos idénticos.

Los poliedros regulares son cinco y sus nombres se forman con un prefijo que indica su número de caras o, lo que es lo mismo, el número de lados del polígono de la base:

• Tetraedro regular: Poliedro con cuatro caras iguales con forma de triángulo equilátero.

• Hexaedro regular (más conocido como cubo): Poliedro con seis caras iguales con forma de cuadrado.
• Octaedro regular: Poliedro con ocho caras iguales con forma de triángulo equilátero.
• Dodecaedro regular: Poliedro con doce caras iguales con forma de triángulo equilátero.
• Icosaedro regular: Poliedro con veinte caras iguales con forma de triángulo equilátero.

2. Poliedros irregulares son aquellos con al menos una cara con una forma poligonal distinta a las demás. Los poliedros irregulares principales son el prisma, la pirámide y el tronco de pirámide.

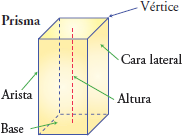
Prisma es aquel poliedro con tres o más paralelogramos como caras laterales y dos poligonales paralelos iguales como base.

Los prismas se clasifican a su vez en distintos tipos según sus propiedades en base a los siguientes criterios:

A) Según la perpendicularidad de las artistas laterales con respecto a las bases:

• Prisma recto es aquel cuyas aristas laterales son perpendiculares a las bases.
• Prisma oblicuo es aquel cuyas aristas laterales no son perpendiculares a las bases siendo sus caras laterales romboidales y sus bases cuadradas.

B) Según la forma del polígono de su base:

• Prisma triangular al ser la base un triángulo.
• Prisma cuadrangular al ser la base un cuadrado.
• Prisma pentagonal al ser la base un pentágono.
• Prisma hexagonal al ser la base un hexágono.
• Etc.

Merece una mención especial el ortoedro (o cuboide), prisma rectangular recto con seis rectángulos por caras, dando lugar únicamente ángulos rectos y siendo las caras opuestas iguales entre sí.

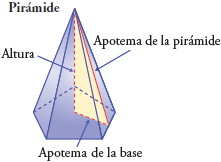
Pirámide es aquel poliedro cuyas caras son triángulos con un vértice común (llamado vértice de la pirámide) y su base un polígono.

Las pirámides se clasifican a su vez según sus propiedades en base a los siguientes criterios:

A) Según el número de lados del polígono de la base:

• Pirámide triangular con un polígono de tres lados como base.
• Pirámide cuadrangular con un polígono de cuatro lados como base.
• Pirámide pentagonal con un polígono de cinco lados como base.
• Pirámide hexagonal con un polígono de seis lados como base.
• Etc.

B) Según la posición del  vértice de la pirámide:

• Pirámide recta es aquella en la que el vértice de la pirámide coincide con la perpendicular que pasa por el centro de su base siento esta un polígono regular.
• Pirámide inclinada (u oblicua) es aquella en la que el vértice de la pirámide no condice con la perpendicular que pasa por el centro de su base.

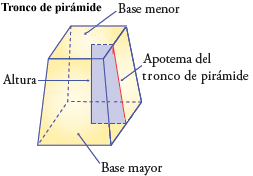
Tronco de pirámide, o pirámide truncada, es el poliedro que se obtiene cuando una pirámide ha sido cortada por un plano. Se diferencian dos tipos según la posición de este plano de corte con respecto a la base:

• Tronco de pirámide recto es aquel en el que el plano de corte es paralelo a la base de la pirámide.
• Tronco de pirámide oblicuo es aquel en el que el plano de corte no es paralelo a la base de la pirámide.

Cuerpos redondos: Definición y nombres

Cuerpo redondo es el cuerpo geométrico delimitados por al menos una superficie curva. También se conocen como sólidos de revolución a aquellos cuerpos redondos delimitados por una figura geométrica plana que gira 360º.

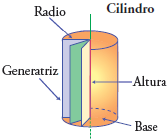
Cilindro es el cuerpo redondo delimitado por dos bases circulares y una superficie curva continua.

• Cilindro rectangular es aquel cuyo eje es perpendicular a sus bases.
• Cilindro oblicuo es aquel cuyo eje no es perpendicular a sus bases.

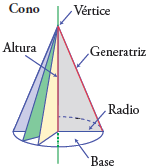
Cono es el cuerpo redondo  delimitado de una base circular o elíptica y una superficie curva que se une en un vértice.

• Cono recto es aquel en el que su eje de revolución es perpendicular a su base y coincide con la altura de su vértice.
• Cono oblicuo es aquel cuyo eje de revolución no coincide con la altura del vértice ni es perpendicular a su base.

Tronco de cono, o cono truncado, es el cuerpo redondo que se obtiene al cortar un cono por uno o dos planos siendo estos perpendiculares a su eje (tronco de cono recto) o no (tronco de cono oblicuo).

Esfera es el cuerpo redondo que es circular en todos sus planos.

Semiesfera es el cuerpo geométrico que se obtiene al cortar una esfera por uno de sus planos obteniéndose un cuerpo redondo compuesto de una base circular y una cúpula esférica.

Teorema de Euler En todos los poliedros convexos se verifica que Caras + Vértices = Aristas + 2 C + V = A + 2
	Tetraedro Pirámide triangular C = 4 V = 4 A = 6
	Cubo Hexaedro C = 6 V = 8 A = 12
	Octaedro C = 8 V = 6 A = 12
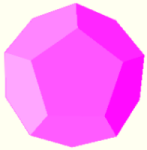	Dodecaedro C = 12 V = 20 A = 30
	Icosaedro C = 20 V = 12 A = 30
	Ortoedro Paralelepípedo Prisma rectangular C = 6 V = 8 A = 12
	Prisma triangular
	Prisma cuadrangular Ortoedro Paralelepípedo
	Prisma pentagonal
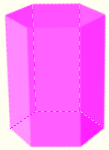	Prisma hexagonal
	Pirámide triangular
	Pirámide cuadrangular
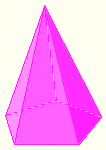	Pirámide pentagonal
	Pirámide hexagonal
	Tronco de pirámide triangular
	Tronco de pirámide cuadrangular
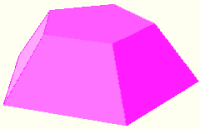	Tronco de pirámide pentagonal
	Tronco de pirámide hexagonal
	Cilindro C = 2 V = 0 A = 0
	Cono C = 1 V = 1 A = 0
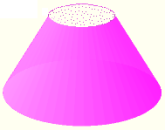	Tronco de cono C = 2 V = 0 A = 0
	Esfera C = 0 V = 0 A = 0

Ejercicios